OliForum Matematico

dimostrare che:



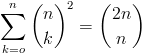
per ogni n intero positivo

gibo92 ha scritto:dimostrare che:



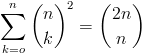
per ogni n intero positivo

Hai hostato un immagine della formula?

Un consiglio: impara il LaTeX. Non è difficile
$ $ \sum_{k=0}^n {n \choose k}^2 = {2n \choose n} $

Io conosco questa:

$ $(a-b)^{2n}= \sum_{i=0}^n {2n \choose i}a^i(-b)^{2n-i} $

Quindi il coefficente di $ a^n(-b)^n $sarà $ $2n \choose n $

Ma $ $(a-b)^{2n}=(a-b)^n(a+b)^n= \sum_{i=0}^n {n \choose i}a^i(-b)^{n-i} \sum_{j=0}^n {2n \choose j}a^jb^{n-j} $
E il coefficiente di $ a^n(-b)^n $ sarà $ $\sum_{i,j\geq0\ i+j=n}^n {n \choose i}{n \choose j}=\sum_{i=0}^n {n \choose i}^2 $

Poichè $ ${n \choose i} = {n \choose n-i} $

E quindi

$ $ \sum_{i=0}^n {n \choose i}^2 = {2n \choose n} $

Qui c'è una generalizzazione

viewtopic.php?t=4391
viewtopic.php?t=12778
viewtopic.php?t=14572

Minuscolo errore: nella quarta riga di Jessica92 c'è un + per un-.