OliForum Matematico

Trovare la probabilità che, presi tre punti a caso su una circonferenza, il triangolo avente per vertici quei tre punti è acutangolo.

Ok, cambiando completamente idea ( e riadottando la prima in assoluto che mi era venuta in mente) e sperando di non dire una scemenza scrivo che:
allora, presi due punti $A$ e $B$ a caso sulla circonferenza si ha che il punto che rispetta le condizioni che cerchiamo appartiene all'arco $A'B'$, dove $A'$ è il simmetrico di $A$ rispetto al centro della circonferenza. Detto ora $\pi k$ l'angolo $\hat{AOB}$ si ha quindi che i casi favorevoli sono proprio $\pi k$. i casi possibili sono banalmente $2 \pi$ e quindi la probabilità al variare di $k$ è pari a $\int_{0}^1 \frac{k}{2} dk = \frac{1}{4}$

(i miei orari sono sempre i migliori xd)

ok, la soluzione è giusta; si poteva anche non usare l'integrale dato che era l'area sottesa ad una retta (così spaventi chi non conosce gli integrali); comunque la soluzione è corretta; ce ne sarebbe anche un'altra con l'utilizzo dei limiti per poligoni di n lati con n tendente a infinito, se qualcuno magari vuole tentarci è carino pure quello come risultato.

e adesso volevo mettere un bel rilancio, anche se non so se sia fattibile, poichè non ho ancora trovto la soluzione e penso richieda qualche strumentino in più (forse andrebbe postato in matematica non elementare, bo...):

Trovare la probabilità che, presi tre punti a caso su una sfera, il triangolo avente per vertici quei tre punti è acutangolo.
Su forza, qualcuno mi illumini sul come fare che ci sto penando su da un po'

Ci ho pensato al rilancio questa notte, mi sembra fattibile, basta usare una tecnica simile a quella che abbiamo usato ora, solo su un fascio di circonferenze... Mah, ora devo andare a scuola, ci penso e in giornata se la trovo posto una soluzione...

allora...

fissiamo due punti sulla sfera $A$ e $B$. Costruito il fascio di piani a cui appartiene $AB$, si vede che abbiamo una famiglia di circonferenze date dall'intersezione di questo fascio di piani con la sfera. Possiamo vedere che per ogni circonferenza di questa famiglia l'angolo $\hat{AOB}$, dove $O$ è il centro della circonferenza presa in considerazione, è compreso tra $\pi$ e $\alpha$. ma $\alpha$ varia tra $0$ e $\pi$ quindi possiamo dire che i "casi favorevoli" sono in tutto

$\int_{0}^{\pi}\int_{\alpha}^{\pi}\frac{\pi x}{2 \pi} \mbox{dx d}\alpha$
( l'argomento dell'integrale più interno è giustificato dal ragionamento del problema in due dimensioni)
Svoglendo i calcoli e tenendo da conto che i "casi favorevoli" sono $4\pi$, si ha che


$p= \frac{\int_{0}^{\pi}\int_{\alpha}^{\pi}\frac{\pi x}{2 \pi} \mbox{dx d}\alpha}{4\pi} = \frac{\frac{1}{4}\int_{0}^{\pi}\pi^2-\alpha^2d\alpha}{4\pi} = \frac{1}{24}\pi ^2$

Bon, probabilmente è sbagliato e non si capisce niente... non abbiate indugio a chiedere.

anche a me viene 1/4...però ho fatto un ragionamento diverso e forse un po' stupido

Siamo tutti concordi sul fatto che esistano 2 modi... posta la tua soluzione

beh...la mia idea è questa.
Fissati 2 punti A e B come in figura ne consegue che la probabilità che sia acuto è data dal rapporto dell'arco Blu (che sarebbero le posizioni di C che consentono al triangolo di essere acuto) con l'intera circonferenza.

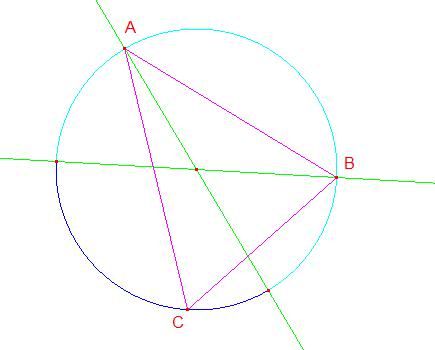
detto questo ho fatto un ragionamento di questo tipo.
i 2 casi limite (delle grandezze dell'arco blu) sono A coincidente con B e A e B diametralmente opposti. gli altri sono intermedi . se facciamo la "media" tra i rapporti di questi archi con la circonferenza otteniamo 1/4... non so se mi sono spiegata
potrebbe andare?

Il tuo ragionamento è giusto per questo caso, ma credo che tu l'abbia fatto giusto senza però prendere in considerazione un fatto
Questo perchè, tu puoi dire ciò, ed è giustissimo, specificando però che quel rapporto di cui tu parli varia secondo una funzione lineare, e quindi per funzioni lineari è proprio come dici tu, basta fare la media;

purrtroppo però il tuo ragionamento non andrebbe bene se quel rapporto variasse tra 0 e 1/2 in maniera non lineare (e qui ci sarebbero un po' di concetti di analisi che non so se sai), in questo caso la tua soluzione sarebbe sbagliata; quindi attenta (o attento, non so ahaha) a utilizzare queste cose

EDIT: ma tu hai fatto i rapporti tra i due archi (1) o hai fatto il rapporto tra l'arco favorevole e la circonferenza (2)? perchè se hai fatto la (1) è sbagliato, se hai fatto la (2) è giusto (alla luce di tutte le considerazioni fatte sopra in questo post...)

EDIT: per quanto riguarda il problema della sfera, non sono certissimo che sia giusto, cioè, sembra filare, ma ho qualche dubbio, spero che qualcuno un po' più esperto magari possa darci il suo parere

no non so quasi nulla di analisi...diciamo che ho ragionato assegnando ad ogni posizione di A B quella corrispondente...cioè...A coincidente B corrisponde ad A e B diametralmente opposti...e cosi via...mi sembra ovvio che il rapporto rimanga costante.
comunque avevo considerato la (2)
grazie x la risposta

ma per me l'idea di fondo di kakkarone93 è giusta, va solo aggiustata un po', è difficile da dire rigorosamente...

a tre dimensioni... bo, è in corso una discussione con <enigma> ( che sta tentando di verificare al computer la soluzione numerica, ma c'è qualche inconveniente...)

Concettualmente mi sembra giusto

ho ripensato alla tua risposta mist, e penso sia errata; ti spiego il motivo lo posto perch vorrei tanto rilanciare il problema; fatto sta che, fissato un punto A sulla sfera, tu avrai solamente un punto (quello diametralmente opposto) che si trova a distanza 2r, avrai infiniti punti che si trovano a distanza r, ne avrai infiniti (ma molti meno, un luogo molto più piccolo) che si trovano a distanza 1/100 r; questo lo puoi vedere tracciando un diametro e tutte le circonferenze in cui il diametro pasa perpendicolare al centro, e ogni circonfrenza è un luogo dei punti equidistante da A kr, con k che varia, ma essendo queste circonferenze di misure diverse in base alla loro posizione, la misura kr non varia linearmente, e quindi non puoi applicare in tale maniera l'integrale;
almeno questo è quello che penso io, ma sono benissimo pronto a ricredermi (magari ho fatto qualche considerazione errata)...

In sintesi, mi stai dicendo che l'errore è nell'utilizzare l'integrale sull'intersezione del fascio di piani con la sfera ? Secondo te in altre parole dovrei cercare una relazione non lineare tra l'angolo che crea il piano considerato con il piano perpendicolare al piano a cui appartiene la circonferenza da cui si genera il fascio e la lunghezza della generica circonferenza generata sul piano ? Giusto per capire cosa secondo te sbagliato...

mm, non ho capito bene il tuo ultimo punto, comunque credo di si, perchè tu utilizzi l'integrale esterno come se fosse per una funzione lineare, ma il fatto è, secondo quello detto sopra, che non mi pare sia lineare, solo che comincio a non capirci più nulla XD

In altre parole tu dici che la lunghezza della circonferenza al variare dell'angolo $\alpha$ non varia linearmente, che in effetti è vero, eprchè pe carnot si ha che $AB = \sqrt{2-2\cos{\alpha }}$... ma questo costituisce realmente un intralcio per ciò che vogliamo noi ? a me lascia più perplesso l'applicazione di un integrale alle "circonferenze rotanti"... Comunque mi sembra che il raggio non influenzi il nostro problema perchè tanto si semplifica (magari sto dicendo una boiata...)