Per prima cosa cambio le lettere, perdonatemi, ma non vorrei incasinare tutto più di quanto già non lo sia con un mare di typo...
Si consideri unt riangolo $ABC$. Siano $D$ e $E$ il circocentro e l'ortocentro di $ABC$. Siamo $F$ e $G$ i punti medi di $AE$ e $CE$. Sia $A'$ il simmetrico di $A$ rispetto a $D$. La tesi è $2GA'$ =$BC$.
Dimostrazione:
Fatto 1: Se $FEDG$ è ciclico, allora $FEDG$ è un trapezio isoscele. Dimostrazione fatto 1: Detto $M$ il punto medio di $DE$, si ha che $MF=MG$ in quanto $M$ è il centro della circonferenza di Feuerbach di $ABC$ a cui appunto appartengono $F$ e $G$. Si deve avere quindi che $ED//FG$ e da questo consegue il Fatto 1.
Sia $L$ il punto medio di $BC$- Per costruzione stessa di $D$ si ha che $BC\perp DL$ e che quindi, detto I il piede dell'altezza che parte da $A$, si ha che $DL//EI$.
Fatto2: $DL=DG$. Dimostrazione Fatto2: Sia $Q$ il punto medio di $AB$ e $H$ il piede dell'altezza da $C$. Per il teorema di talete si ah che $FG//QL$ e $FQ//GL$. Inoltre, sempre per Talete, si ha che $FQ//EB\perp AC//FG$ e quindi $FQ\perp FG$ . Si ha quindi che $FQLG$ è un rettangolo. Ricordando che $M$ è il punto medio di $ED$ e che $M$ è equidistante dai lati del rettangolo in quanto centro della circonferenza ad esso circoscritta, si ha quindi il fatto 2.
Siccome per quanto detto $FELD$ è un parallelogramma, si ha che anche $FADL$ lo è e quindi in particolare $FL=AD=A'D$. Sempre per Talete infine si ha che $EL=LA'$, $EL//LA'$. Si ha quindi che i punti $E$, $L$ e $A'$ sono collineari. Di conseguenza, $C$ si rivela essere il simmetrico di $A'$ rispetto ad $ED$ giacchè: $\hat{LED} = \hat{DEG}$ per quanto deto prima ed $EL=LA'=EG=GC$. Allo stesso modo $G$ è il simmetrico di $L$ rispetto alla retta $ED$ e quindi si ha che $DLA'$ è congruente a $DGC$ in quanto uno è il simmetrico dell'altro sempre rispetto a $DE$. Inoltre $LG//A'C\perp DE$ e quindi $LGA'C$ è un trapezio isoscele. In particolare quindi $LGA'=LGC$ e in particolare quindi finalmente $GA'=LC=\frac{BC}{2}$ che è la tesi.
Spero d'averci preso

p.s. scusate per la figura incasinata

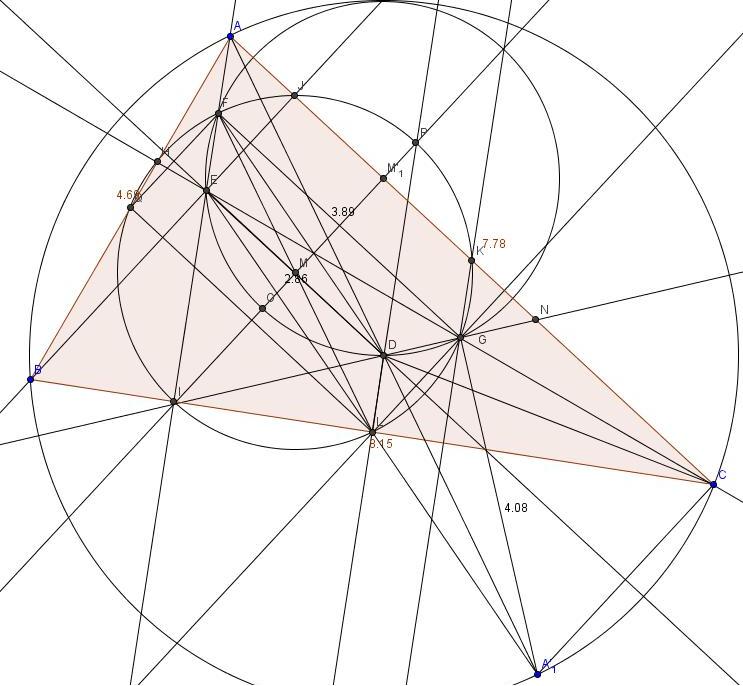
- Staffetta
- 250791_174156555975860_100001445516759_460384_8077489_n.jpg (71.63 KiB) Visto 1461 volte
Corretto i typo, grazie della segnalazione
