rette parallele e triangolo equilatero.

[Mike]

Abbiamo tre rette parallele $ s $, $ t $ e $ v $. $ s $ e $ t $ distano 1, $ t $ e $ v $ 2, $ s $ e $ v $ 3. Quanto vale il lato del triangolo equilatero avente i tre vertici appartenenti ciascuno ad una retta?

[Karl Zsigmondy]

Sia A il vertice su s, B il vertice su T, C il vertice su v. Sia D la proiezione di A su v, E la proiezione di B su v, F la proiezione di B su S. Se chiamo DC=x e CE=y e applico Pitagora ai triangoli ADC, CEB, BFA ottengo che il quadrato del lato del triangolo equilatero in questione è uguale rispettivamente a:
$ x^2 + 9 $
$ y^2 + 4 $
$ x^2 + 2xy + y^2 + 1 $
Dalle prime due ottengo che $ y=\sqrt{x^2+5} $. Dato che l'espressione ottenuta sottraendo la terza alla somma delle prime due è ancora equivalente a questa, e dato che è 12-2xy, ora sostituisco il valore di y in funzione di x ed uguaglio il tutto a $ x^2 + 9 $. Alla fine ottengo che $ x^2 = \frac{1}{3} $ da cui $ l=\sqrt{x^2 + 9} = \frac{2\sqrt{21}}{3} $.

[kakkarone93]

Io provo a postare la mia soluzione...


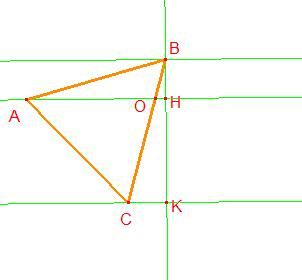
essendo BK perpendicolare al fascio, allora BH=1 e HK= 2. Allora per Talete BO = $ \frac{1}{2} $ OC
sia x il lato del triangolo.possiamo allora dire che
$ BO= \frac{x}{3} $

$ OC=\frac{2x}{3} $

considerando il triangolo ACO => $ AO^2= AC^2+CO^2 -2 CO * AC * cos 60° = x^2+ \frac{4x^2}{9} - \frac{2x^2}{3} = \frac{7x^2}{9} $

$ AO=\frac{x\sqrt{7}}{3} $

considerando il triangolo AHB => $ AH^2 = X^2-1 $

$ AH=\sqrt{x^2-1} $

ora, l'area del triangolo AHB è la somma dei triangoli AOB e OHB
quindi $ \frac{AH * HB}{2} = \frac{1}{2} * AB * BO* sin 60° + OH * BH * \frac{1}{2} $ essendo OH= AH-AO
$ \frac{\sqrt{x^2-1}}{2} = \frac{1}{2} x \frac{x}{3} \frac{\sqrt{3}}{2} + (\sqrt{x^2-1}-\frac{x\sqrt{7}}{3}) \frac{1}{2} $

Che risolvendo viene $ x=0 \lor x= \frac{2\sqrt{21}}{3} $

dove ho sbagliato???

[Karl Zsigmondy]

Non hai sbagliato da nessuna parte, avevo sbagliato a fare la radice di 28/3. Ora ho corretto anche la mia.

[ale.G]

Penso di aver trovato l'inghippo...karl ha semplicemente sbagliato a fare l'ultimo conto...se $x^2=\frac{1}{3}$ allora $l=\frac{2\sqrt{7}}{\sqrt{3}}$, che è uguale al risultato di kakkarone


karl mi ha anticipato di un secondo...

[kakkarone93]

oook! grazie mille