OliForum Matematico

Premettendo che non l'ho risolto:
È possibile suddividere un quadrato di lato intero in più quadrati di lato intero, in modo che non ci siano due quadrati aventi un lato della stessa lunghezza?
Se si, l'affermazione di sopra è vera anche per i cubi?
Tecnicamente MNE:Per "induzione", qual è il minore n tale che un ipercubo in n dimensioni NON si può suddividere in ipercubi più piccoli di lato diverso? Oppure si può sempre fare?

karlosson_sul_tetto ha scritto: È possibile suddividere un quadrato di lato intero in più quadrati di lato intero, in modo che non ci siano due quadrati aventi un lato della stessa lunghezza?

Sì, è possibile, però non con tutti i quadrati. Martin Gardner ci ha dedicato un intero capitolo in "Enigmi e giochi Matematici". Il più piccolo quadrato di lato intero che possa essere diviso in quadrati di lati tutti diversi che è stato trovato finora è di lato 175 ed è formato da 24 quadrati di lato intero e tutti diversi tra loro.

(Non avevo visto la tua risposta fino ad adesso, scusa)
Wow, non lo sapevo, nonostante abbia il suddetto libro di gardner a casa grazie mille per la risposta!

Quindi il problema "olimpico" che rimane è: è possibile tassellare un cubo con cubi più piccolo tutti diversi tra loro?

Per i cubi, con qualche imbroglio sottile, forse la si può vedere così

Uhm, sbaglio o il tuo metodo funzionerebbe senza i problemi anche con i quadrati (sui quali sappiamo che esiste una tassellazione...)?
Anche perché non mi convince troppo il fatto che il cubetto più piccolo resta sempre indietro

No, forse ho scritto male Prima tassello solo il primo strato, cioè mi scelgo una faccia del cubo (il pavimento) e la ricopro di cubetti in modo che non ci siano buchi. Quindi come minimo sto già supponendo di poter tassellare coi quadrati. Per ora non c'è nessun cubetto sopra altri, ho fatto solo uno strato.
Ora da qui vedo dov'è il cubo più piccolo, che essendo il più piccolo crea un "vuoto" sopra di esso visto che i vicini sono più alti. Quindi quando voglio fare il secondo strato (ovvero mettere un'altro strato di cubetti sopra quelli che ho già messo), tutto ciò che metto sopra quel cubetto è separato dal resto (visto che altrimenti rimarrebbe uno spazio vuoto). Quindi posso ripetere il ragionamento coi cubetti da mettere sopra il cubetto più piccolo della volta precedente.

PS: per sopra intendo in verticale, in altezza, forse era lì il punto

Quello che volevo dire io è: guarda il problema dei quadrati.
Prendi un quadrato e prima "tassella" lo strato più basso, ovvero scegli un lato e metti i quadrati a lui adiacenti; anche qua ne avrai uno più piccolo degli altri. Anche questo crea un vuoto che secondo il tuo ragionamento non potrebbe essere riempito perché ad ogni passaggio rimarrebbe sempre più indietro rispetto ai due adiacenti. Cioè, puoi usare la stessa idea/ragionamento per dimostrare l'impossibilità di tassellare un quadrato, ma dato che un quadrato si può tassellare...

Ok, ho capito cosa vuoi dire. Sono stato superficiale in pratica La differenza sta nel fatto che coi quadrati, il quadrato più piccolo di una "striscia" lo puoi trovare pure al bordo della striscia. Quindi il "vuoto" può essere colmato senza creare altri "vuoti" interni. Esempio: guarda cosa succede in basso a sinistra in questa figura:


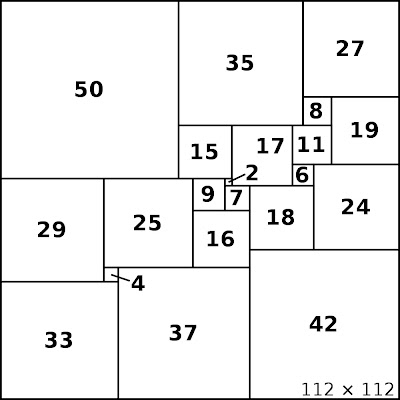
Coi cubi invece il "vuoto" è sempre interno alla regione che sto considerando. (Si vede che sullo stesso piano il cubo più piccolo non può capitare ai bordi), e questo fa sì che salendo in altezza capita sempre una regione "affossata" rispetto a quelle circostanti che non può essere colmata da cubi messi in regioni diverse, cosa che coi quadrati può accadere visto che se il più piccolo capita sul bordo può essere colmato dai quadrati della regione vicina.

Ok, ho capito quello che volevi dire.
Diciamo che come tutta la tua C è molto ideofila e formalizzaziofoba, ma ciò non toglie la sua semplicità. Great