Pagina 1 di 1
Linee di campo
Inviato: 27 ott 2006, 19:42
da luca88
Ciao a tutti!
Ho una domanda che vi sembrerà banale, ma non lo è per me quindi scusatemi!!
Una carica che viene posta in un campo elettrico segue una traiettoria che è indicata dalla linee di campo? Oppure queste servono solo per dare un'indicazione generale di come è fatto il campo?
Grazie!!

Inviato: 27 ott 2006, 20:21
da Bolzo88
La seconda che hai detto.
La traiettoria non segue le linee di campo per una ragione molto semplice: immagina un corpo posto su una linea di campo curva con velocità tangente alla linea stessa. Nel punto in cui si trova il corpo la forza, essendo parallela alla linea di campo, è parallela alla velocità, quindi non produce accelerazione radiale, quindi non può fare in modo che la traiettoria segua la curva.
Inviato: 27 ott 2006, 21:39
da MateCa
Esiste solo un caso particolare in cui le linee di campo coincidono con la traiettoria: campo elettrico uniforme (quindi con linee di campo rette e parallele fra loro) e carica inizialmente ferma o in moto lungo la direzione delle linee di campo.
Inviato: 29 ott 2006, 00:32
da ¬[ƒ(Gabriel)³²¹º]¼+½=¾
Difatti data una carica elettrica puntiforme q in moto con velocità

in una regione caratterizzata dalla presenza di un campo di induzione magnetica
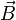
, sulla suddetta carica agirà una forza

, detta appunto Forza di Lorentz, proporzionale a q stessa e al prodotto vettoriale di

per
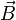
, secondo la seguente formula:

quindi nel caso in cui una carica entra parallelamente alle linee di campo, su di essa non agirà la forza di lorenz perchè sen0=0
Inviato: 29 ott 2006, 14:40
da NEONEO
SCusate ma non sono molto d'accordo con quanto avete detto. Infatti immaginiamo che una carica positiva sia posta nello spazio e ivi mantenuta.. Ora pongo ad una certa distanza da essa un'altra carica positiva. Cosa succede? Succede che la seconda carica positiva si muoverà di moto acclerato lungo la linea di campo generato dalla prima carica. Se per assurdo esistesse un campo elettrico curvo generato da uin'ipotetica configurazione di cariche, una carica positiva campione posta in esso si muoverà esattamente seguendo le linee di campo al contrario di quanto dicevate voi, proprio per il fatto che la linea di campo indica modulo direzione e verso del vettore forza nello spazio e quindi anche la traiettoria di un oggetto cui questa forza è applicata. Un altro esempio banale è un sasso che cade: non segue forse le linee di campo gravitazionale?
non le segue solo se ha velocità inizial perpendicolare alle linee di campo non nulla, e in particolare si creerà una parabola. Lo stesso avviene per il campo elettrico. Diverso è invece il caso del campo magnetico che dipende dalla velocità di una particella e la forza è sempre perpendicolare al vettore velocità. in questo caso è evidente che il ragionamento fatto qui sopra non vale più.
Inviato: 29 ott 2006, 14:51
da Nonno Bassotto
NEONEO ha scritto:Se per assurdo esistesse un campo elettrico curvo generato da uin'ipotetica configurazione di cariche, una carica positiva campione posta in esso si muoverà esattamente seguendo le linee di campo al contrario di quanto dicevate voi, proprio per il fatto che la linea di campo indica modulo direzione e verso del vettore forza nello spazio e quindi anche la traiettoria di un oggetto cui questa forza è applicata. Un altro esempio banale è un sasso che cade: non segue forse le linee di campo gravitazionale?
Ti sei dato un controesempio da solo. Il sasso che cade segue le linee di forza solamente se non parte con una certa velocità orizzontale. Nel caso in cui le linee di forza non siano tutte rette parallele, non le seguirà nemmeno partendo da fermo, come già spiegato sopra. Se una particella segue una linea di campo, non riceve accelerazione ortogonale alla linea di campo. Quindi non può curvare.
Inviato: 29 ott 2006, 14:53
da NEONEO
Credo che tu stia sbagliando per il fatto che può invece curvare benissimo in quanto è la forza stessa che determina la traiettoria e con essa la velocità, non il contrario....

Inviato: 30 ott 2006, 13:03
da Nonno Bassotto
La forza determina l'accelerazione, non la velocita'!!!
Inviato: 30 ott 2006, 22:34
da Bolzo88
NEONEO ha scritto:Credo che tu stia sbagliando per il fatto che può invece curvare benissimo in quanto è la forza stessa che determina la traiettoria e con essa la velocità, non il contrario....

Vediamo se riesco a fartela capire con un altro ragionamento (senza togliere validità a quelli espressi in precedenza da me e Nonno Bassotto). Mettiti in una qualsiasi disposizione di cariche che generi linee di campo curve. Metti una carica su una linea di campo con velocità iniziale parallela alla linea stessa. Se cambio il modulo della velocità iniziale mi cambierà la traiettoria del moto? Direi che possiamo ragionevolmente supporre di sì. Ma se il modulo della velocità iniziale influisce sulla traiettoria, significa che essa non è unica, e che quindi non può seguire in ogni caso la linea di campo.
In altre parole, non è solo la forza che determina la traiettoria, che è invece influenzata anche dalla velocità (e dalla massa del corpo).
Per correggere un'imprecisione di MateCa: non è necessario che le linee di forza siano tutte parallele tra di loro, basta che siano rettilinee (pensa al campo generato da una carica puntiforme).
Inviato: 31 ott 2006, 18:36
da MateCa
Scusate, mi sono spiegato male.
Se la carica inizialemente è ferma, è sufficiente che le linee di campo siano rettilinee, come suggeriva Bolzo88.
Ma se la carica ha velocità iniziale non nulla, deve avere una velocità parallela alla linea di campo su cui giace.
Quindi ci sono 2 casi
1) la velocità è parallela alle linee di forza di un campo uniforme
2) la velocità deve essere diretta parallelamente alla linea di campo su cui giace. Nel caso della carica puntiforme, anche se le linee di campo sono rettilinee, la carica può percorrere una traiettoria che non segue le linee di campo se si trova su una linea di campo non parallela alla sua velocità.
Spero di essermi spiegato.
Inviato: 02 nov 2006, 14:08
da NEONEO
Si, scusate, non è che seguono per forza le linee di campo però certamente esse determninano l'andamento della traiettoria. Alla fine quello che contava sottolineare è che le linee di campo danno informazioni anche sull'evolversi della traiettoria. Comunque è vero, che non conincide con esse, scusate.

 in una regione caratterizzata dalla presenza di un campo di induzione magnetica
in una regione caratterizzata dalla presenza di un campo di induzione magnetica 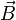 , sulla suddetta carica agirà una forza
, sulla suddetta carica agirà una forza  , detta appunto Forza di Lorentz, proporzionale a q stessa e al prodotto vettoriale di
, detta appunto Forza di Lorentz, proporzionale a q stessa e al prodotto vettoriale di 