Ok...mi scuso se ho utilizzato una metodologia che magari non perfettamente si addice ad un forum di fisica che mira più all'originalità che ad un brutale utilizzo di formule. Per cui attuo un diverso approccio che non richiede particolari conoscenze.
Supponiamo quindi di non conoscere la formulazione in termini di coordinate polari dell'ellisse e della formula di Binét che ho in parte dimostrato nei punti 8 ) e 9) del mio precedente messaggio. Supponiamo ancora che il corpo B di massa $ $M$ $ non si muova affatto, per cui trascuriamo la massa ridotta $ $\mu$ $ e consideriamo la massa propria $ $m$ $ di A.
Resta comunque la problematica di definire il momento angolare del sistema in funzione delle sue caratteristiche e di definire la posizione del corpo in funzioni di coordinate spaziali più che temporali (il sistema di riferimento è lo stesso del messaggio precedente).
Per ciò che riguarda il momento angolare, uguagliamo l'energia del corpo A all'afelio e al perielio, e esprimiamo le relative velocità in funzione del momento angolare della massa e della distanza. In formule;
$ $\begin{displaymath}
\left\{
\begin{array}{ll}
\frac{1}{2}m{v_a}^{2}-G\frac{Mm}{r_a}=\frac{1}{2}m{v_p}^{2}-g\frac{Mm}{r_p} \\
L=mr_a{v_a}=mr_pv_p
\end{array}
\right.
\end{displaymath}
$ $
Da cui si ricava facilmente che;
$ $\begin{displaymath}
L^{2}=GMm^{2}\frac{2}{r_p+r_a}r_pr_a=G\frac{Mm}{a}r_ar_p
\end{displaymath}$ $
e osservando che;
$ $\begin{displaymath}
\left\{
\begin{array}{ll}
r_a=a+c \\
r_p=a-c
\end{array}
\right.
\end{displaymath}$ $
si ha;
$ $\begin{displaymath}
L^{2}=G\frac{Mm^{2}}{a}b^{2}
\end{displaymath}$ $
dove $ $b$ $ è il semiasse minore.
L'energia è, come prima;
$ $\begin{displaymath}
E=\frac{1}{2}m\left(v_t^{2}+v_r^{2}\right)-G\frac{Mm}{r}
\end{displaymath}$ $
La componente tangenziale la possiamo esprimere nel seguente modo;
$ $\begin{displaymath}
v_t=\frac{L}{mr}
\end{displaymath}$ $
mentre la componente radiale necessita del calcolo della derivata temporale di $ $r$ $. Per fare ciò mi ricavo l'espressione del punto 1) con un ragionamento geometrico e applico il ragionamento effettuato al punto 6) del precedente messaggio.
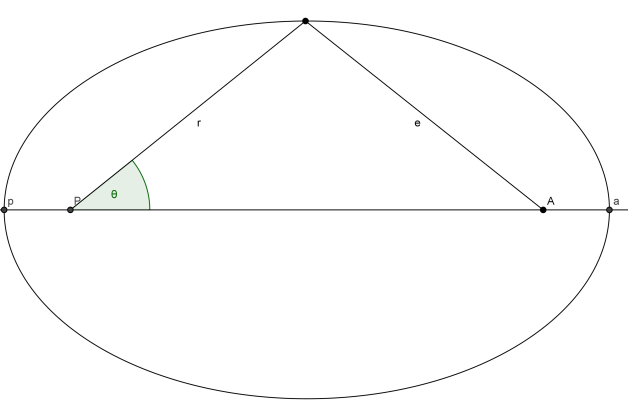
Rifacendomi alla figura nell'allegato, si sa che;
$ $\begin{displaymath}
r+e=2a
\end{displaymath}$ $
e applicando il teorema di Carnot al lato $ $e$ $, si pervinene alla seguente formula;
$ $\begin{displaymath}
\frac{1}{r}=\frac{a}{b^{2}}-\frac{c}{b^{2}}\cos{\theta}
\end{displaymath}$ $
A questo punto si procede come al punto 6) e si ricava il valore dell'energia.