La ricerca ha trovato 10 risultati
- 21 ott 2008, 15:48
- Forum: Cultura matematica e scientifica
- Argomento: Riforma "scolastica"
- Risposte: 46
- Visite : 30412
- 19 ott 2008, 17:31
- Forum: Cultura matematica e scientifica
- Argomento: Riforma "scolastica"
- Risposte: 46
- Visite : 30412
Re:
@ SkZ: penso che EUCLA ti stesse chiedendo se lo hai saputo attraverso il forum: ritiene improbabile che nei giornali locali chileni (ma davvero stai in chile?!) ne abbian parlato
@ EUCLA: beh l'idea che dei nick del forum si materializzeranno nelle mie vicinanze è per me come benzedrina, suppongo ...
@ EUCLA: beh l'idea che dei nick del forum si materializzeranno nelle mie vicinanze è per me come benzedrina, suppongo ...
- 18 ott 2008, 22:32
- Forum: Cultura matematica e scientifica
- Argomento: Riforma "scolastica"
- Risposte: 46
- Visite : 30412
martedi 21 ottobre
se ne avete bisogno, ecco una mappa con segnalati quasi tutti i dipartimenti, forse non tutti sono al posto giusto 8) inoltre non so dove siano dislocati i vari plessi di medicina.
ci sono pure le mense A.R.D.S.U. che in teoria dovrebbero offrire agli studenti (universitari) non fiorentini un pasto ...
ci sono pure le mense A.R.D.S.U. che in teoria dovrebbero offrire agli studenti (universitari) non fiorentini un pasto ...
- 12 gen 2006, 10:32
- Forum: Cultura matematica e scientifica
- Argomento: Transolimpiadicus
- Risposte: 5
- Visite : 6499
hojas de coca descocainizadas
in quel "qualunque cosa" io ho messo:
-analisi: "a course of modern analysis" watson & whittaker (vecchietto e manipolativo)
-algebra: "algebra" michael artin, non enciclopedico... ~cerca di trasmettere il senso dell'algebra
-topologia: "topologia" janich, dà una panoramica... poi singer & thorpe ...
-analisi: "a course of modern analysis" watson & whittaker (vecchietto e manipolativo)
-algebra: "algebra" michael artin, non enciclopedico... ~cerca di trasmettere il senso dell'algebra
-topologia: "topologia" janich, dà una panoramica... poi singer & thorpe ...
- 14 set 2005, 21:07
- Forum: Geometria
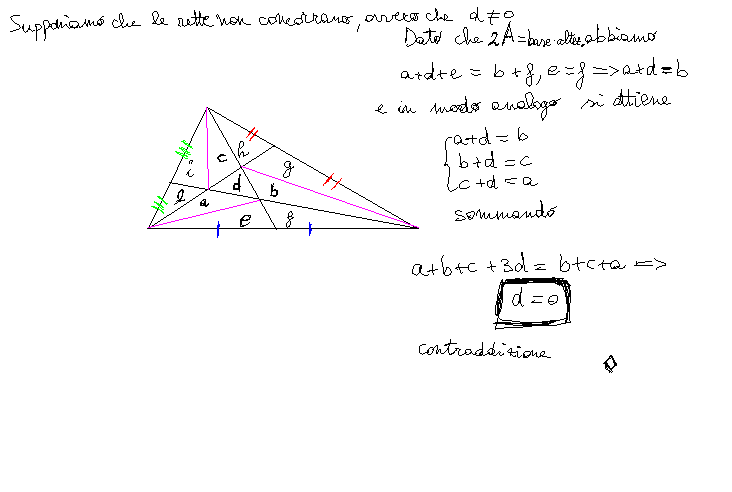
- Argomento: mediane per assurdo
- Risposte: 5
- Visite : 6315
- 14 set 2005, 15:42
- Forum: Teoria dei Numeri
- Argomento: 1/a+1/b=1/c
- Risposte: 8
- Visite : 6283
gcd(x1,...,xn)
(magico è solo CAUCHY-SHWARTZ).
usando la notazione english-style di LeLe,
\displaystyle gcd(x_1,...,x_n)\prod_{j=1}^n{\prod_{1\le i_1 <...<i_j \le{n}}lcm(x_{i_{1}},...,x_{i_{j}})^{(-1)^{j}}}=1
ma devo andare al budokan... comunque in breve, ordinando gli esponenti dei numeri primi in cui si ...
usando la notazione english-style di LeLe,
\displaystyle gcd(x_1,...,x_n)\prod_{j=1}^n{\prod_{1\le i_1 <...<i_j \le{n}}lcm(x_{i_{1}},...,x_{i_{j}})^{(-1)^{j}}}=1
ma devo andare al budokan... comunque in breve, ordinando gli esponenti dei numeri primi in cui si ...
- 13 set 2005, 23:37
- Forum: Teoria dei Numeri
- Argomento: 1/a+1/b=1/c
- Risposte: 8
- Visite : 6283
con (x_1,...,x_n) indicherò il mcm di x_1, ..., x_n
alor, poniamo x=M.C.D.(a,b) e a=a'x, b=b'x , allora \frac{1}{a'x}+\frac{1}{b'x}=\frac{1}{c} implica c=\frac{a'b'x}{a'+b'}
ora \frac{(a'+b')x}{M.C.D(a'x,b'x,c)}=\frac{(a'+b')x(xa',xb')(xb',c)(xa',c)}{x^2a'b'c(a'x,b'x,c)}= \frac{(a'+b')x(a',b')(xb ...
alor, poniamo x=M.C.D.(a,b) e a=a'x, b=b'x , allora \frac{1}{a'x}+\frac{1}{b'x}=\frac{1}{c} implica c=\frac{a'b'x}{a'+b'}
ora \frac{(a'+b')x}{M.C.D(a'x,b'x,c)}=\frac{(a'+b')x(xa',xb')(xb',c)(xa',c)}{x^2a'b'c(a'x,b'x,c)}= \frac{(a'+b')x(a',b')(xb ...
- 07 set 2005, 16:12
- Forum: Algebra
- Argomento: Coseni, che passione!
- Risposte: 9
- Visite : 10444
ma questo problema ha una fonte o è originale?
sì, la formula che chiedeva simo non comprendeva la somma che hai scritto.
perché nel momento in cui n divide a cambia il risultato e cambia ogni volta che n divide un a-2j in più...
ad esempio, sia a=10.
se n=10, il risultato è \frac{\binom{10}{5}+2}{2^{10}}n perché n divide 10, mentre se n=8 ...
perché nel momento in cui n divide a cambia il risultato e cambia ogni volta che n divide un a-2j in più...
ad esempio, sia a=10.
se n=10, il risultato è \frac{\binom{10}{5}+2}{2^{10}}n perché n divide 10, mentre se n=8 ...
- 07 set 2005, 14:26
- Forum: Algebra
- Argomento: Coseni, che passione!
- Risposte: 9
- Visite : 10444
concordo col titolo (da un punto in poi)
ma per a=2 ci interessa il primo termine, che è \frac{1}{2}n
(ovvero, \frac{\binom{a}{a/2}}{2^a}n )
anch'io suddivido in pari e dispari, con dispari nulli...
magari ha fatto confusione il fatto che io abbia sostituito a con 2a per indicare i numeri pari... la condizione è che 2a<n
o meglio ...
(ovvero, \frac{\binom{a}{a/2}}{2^a}n )
anch'io suddivido in pari e dispari, con dispari nulli...
magari ha fatto confusione il fatto che io abbia sostituito a con 2a per indicare i numeri pari... la condizione è che 2a<n
o meglio ...
- 06 set 2005, 17:15
- Forum: Algebra
- Argomento: Coseni, che passione!
- Risposte: 9
- Visite : 10444
UP UP UP!!!
Su che è divertente!
3. \displaystyle \sum_{k=1}^n \cos^{2a}(\frac {2k\pi}n) = \frac{\binom{2a}{a}}{2^{2a}}n = \frac{\binom{2a-1}{a-1}}{2^{2a-1}}n
@evaristeG: penso anch'io :oops: comunque, l'hint principale del 3. che non distrugge l'1. :
Sia n primo.
\displaystyle \sum_{k=1}^n \cos^{2a ...
3. \displaystyle \sum_{k=1}^n \cos^{2a}(\frac {2k\pi}n) = \frac{\binom{2a}{a}}{2^{2a}}n = \frac{\binom{2a-1}{a-1}}{2^{2a-1}}n
@evaristeG: penso anch'io :oops: comunque, l'hint principale del 3. che non distrugge l'1. :
Sia n primo.
\displaystyle \sum_{k=1}^n \cos^{2a ...