help

[Homer J Simpson]

ho un rettangolo di lato $ b $ e $ a $ con $ a > b $ lo piego lungo la sua diagonale, quantè l'area del triangolo che si è formato?

[<enigma>]

ho un rettangolo di lato $ b $ e $ a $ con $ a > b $ lo piego lungo la sua diagonale, quantè l'area del triangolo che si è formato?

Si è formato più di un triangolo, sii preciso nello scrivere il testo

[Homer J Simpson]

e vero scusa, si formano due triangoli rettangoli e un triangolo isoscele, devo trovare l'area del triangolo isoscele

[Homer J Simpson]

ok, ero sotto la doccia ed ho trovato la risposta

era smplicissimo

[kakkarone93]

beh, la posto lo stesso la soluzione che ho trovato...



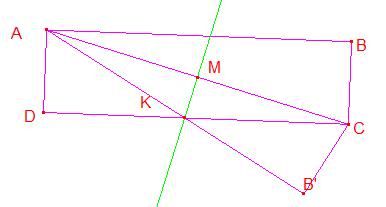
il triangolo AB'C è il simmetrico di ABC (x hp) quindi l'angolo B'AC =CAB. essendo inoltre la retta in MK asse di AC, l'angolo KMA = CBA (retti) quindi AKM è simile a ACB.
detto ciò, AM:AB=KM:BC e troviamo l'altezza del triangolo per base AC : Pitagora (ovviamente )
quindi area= (a^2*b+b^3) / 4a ...
giusto?
(perdonatemi ma non so usare il LATEX... )

EDIT: ho imparato ad usarlo!!! ecco la formula scritta "leggibile" : $ \frac{\left ( a^2 b+b^3 \right )}{4a} $

[paga92aren]

anche a ma viene così

[kakkarone93]

anche a ma viene così

ottimo!