Parallelogramma own

[Mattysal]

Sia $ABCD$ un parallelogramma, denotiamo con $O$ il circocentro di $ABD$ e con $M$ il punto medio di $AD$. Sia $K$ l’intersezione tra la circonferenza circoscritta al triangolo $BCD$ e la circonferenza di diametro $AD$.
Dimostrare che le rette $AK$, l’altezza uscente dal vertice $B$ relativa al triangolo $ABD$ e la retta per $M$ parallela a $BO$ sono concorrenti.

[ricarlos]

Testo nascosto:

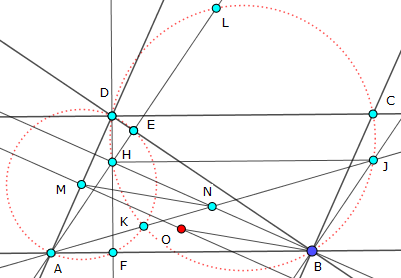
Sia $H$ l'ortocentro di $ABD$.

Usiamo il seguente lemma: il riflesso di $H$ rispetto a $BD$ è sulla circonferenza circoscritta ad $ABD$.
Poiché $(BCD)$ è il riflesso di $(ABD)$ rispetto a $BD$, allora $H$ è sulla $(BCD)$.

Usiamo questo altro lemma: $BH = 2MO$.
Sia $N$ il punto medio di $BH$, quindi $MO = BN$ e poiché $MO\parallel BN$ allora $BO\parallel MN$.

Siano $E$ e $F$, rispettivamente, i piedi delle altezze uscente dei vertici $A$ e $D$ nel triangolo $ABD$, così $A,F,K,E,D$ sono punti conciclici.
Siano $J=AK\cap (BCD)$ e $L=AH\cap (BCD)$.
Dal teorema di Reim $JB\parallel AE$, allora $HBJL$ è un trapezio isoscele $\rightarrow \angle LHJ = \angle BDH$.
Ma $\angle BDH = \angle EDF = \angle EAF \rightarrow \angle EAF = \angle LHJ \rightarrow JH\parallel AB$.
Quindi $ABJH$ è un parallelogramma, allora $AJ$ (o AK) interseca $BH$ in $N$.

paralelo.png (29.48 KiB) Visto 6899 volte