Online World Math Contest 2022 - problem 20

[ronny]

Ciao a tutti. Non riesco a risolvere questo problema. Ho tentato di ragionare
anche con le formule che categorizzano le terne pitagoriche (2mn, m^2-n^2, ecc..), ma senza
successo.
Qualcuno puoi aiutarmi a trovare la soluzione?

Bob has a perfectly semi-circular plot of land, as in the figure, and
wants to divide it into several parts (six) by building two triangular
fences whose common base is the diameter of the semicircle (AB)
and whose other vertices (C and D) are on the semicircle. Bob
wants the two triangles ABC and ABD to be non-congruent, so
triangle ABP is not isosceles.



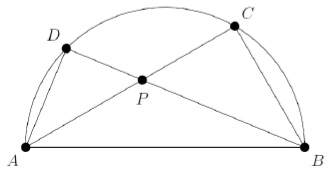
Alice helps Bob and together they build the fences so that the measurements,
in m, of all the (seven) segments visible in the figure,
built between the posts A, B, C, D and P, are expressed by integers.
What is the minimum perimeter, in m, of triangle ABP?

[emmeci]

A meno di idee che proprio non mi vengono, direi che cercare il perimetro minimo è o troppo facile o troppo lungo.
Troppo facile perché il minimo è zero, ottenibile quando tutti i punti coincidono.
Se invece vogliamo che siano tutti distinti, è troppo lungo: occorre fare con pazienza i calcoli con molti valori possibili perché non si può prescindere dai dati numerici. Mi spiego con un esempio: se so solo che a, b sono numeri naturali, posso dire che ab è un loro multiplo comune, ma non che è il loro mcm; per avere il minimo occorre conoscerne i valori.
Rispondo quindi ad una domanda un po' diversa, chiedendomi come si può fare in modo che tutti i sette segmenti abbiano valori interi. Per evitare lunghe formule, faccio il ragionamento su dati numerici, riferiti ad un caso particolare; alla fine, indicherò come generalizzare la risposta.

Ci sono due diversi triangoli rettangoli con lati interi, quindi occorrono due terne pitagoriche e penso a (3,4,5) e (5,12,13). I triangoli debbono avere la stessa ipotenusa e per ottenerlo moltiplico i numeri della prima terna per 13k e quelli della seconda per 5k. Per avere una certa somiglianza con la figura postata ho quindi
[math]AC=4*13k; BC=3*13k; BD=12*5k; AD=5*5k; AB=5*13k
Altre soluzioni possono essere ottenute scambiandi i cateti fra loro, ma non le ho esaminate, salvo scoprire involontariamente che anche con altre figure bisogna badare a quali sono i cateti che si intersecano, pena risultati assurdi.
Posto ora $ \alpha= C \hat A B $; $ \beta=A \hat B D $, dai triangoli rettangoli ABC ed ABD ricavo seno e coseno di $ \alpha,\beta $ e ne deduco il seno di $ A \hat P B=\pi-\alpha-\beta $. Applicando ora il teorema dei seni al triangolo ABP, arrivo a $ AP=\frac {5^3*13} {56}k; BP=\frac {3*5*13^2} {56}k $ e sono interi se $ k=56 $.

Generalizzazione: si può partire dalle terne pitagoriche $ (2mn,m^2-n^2,m^2+n^2), (2pq, p^2-q^2, p^2+q^2) $ moltiplicandone i dati in modo che l'ipotenusa diventi $ k*mcm(m^2+n^2, p^2+q^2) $; se rinuciamo al minimo, basta moltiplicare la prima terna per $ k(p^2+q^2) $ e la seconda per $ k(m^2+n^2) $. Si continua poi come prima, determinando k in modo da semplificare il denominatore; ed anche per questo occorrono i dati numerici perché le frazioni possono semplificarsi e quindi può bastare un valore di k più piccolo.

[ronny]

Bell'approccio, grazie. Quindi se ho capito questa tecnica ci permette di produrre i 7 segmenti interi a partire da una coppia qualsiasi di terne
pitagoriche. Bisogna scoprire quale coppia di terne produce il perimetro minimo.

Il fatto che i due triangoli APD e BPC siano simili (sono rettangoli e i due angoli in P sono opposti al vertice e quindi uguali) può aiutare
all'interno del tuo ragionamento?

Così per curiosità la soluzione è

Testo nascosto:

180

(il problema è capire come arrivarci)

In modo "bovino" ci si può arrivare scrivendosi tutte le terne con numeri non troppo grandi, tipo sotto i 100, 120 per
vedere se la soluzione stia lì dentro (sperando che gli autori non sia così cattivi).
Spulciando tra le terne con l'ipotenusa in comune con un po' di tentativi, considerando anche la similitudine
tra i triangoli che ho indicato, si può arrivare a trovare le terne giuste. Ma non è che sia un'approccio molto elegante.
(mi sono già scordato quali fossero infatti).

[emmeci]

Anche il mio approccio attuale è tutt'altro che elegante, ma trovo una soluzione numerica.
Poiché i triangoli ADP e BCP sono simili, corrispondono ad una stessa terna pitagorica (x,y,z); ho quindi
$ DP=hx; AD=hy; AP=hz; CP=hx; BC=ky; BP=kz $

e si ricava facilmente che $ AB^2 = z[2hkx+z(h^2+k^2)] $
Non saprei come imporre che AB sia intero; usando però la terna x=3; y=4; z=5, andando per tentativi ed aiutandomi col perimetro che indichi, trovo che si ha una soluzione per $ h=9; k=10 $ (o viceversa).
Con questi valori si ottiene AB=85.