come può essere vero?
come può essere vero?
guardate le figure cliccando qui sotto
http://math.stanford.edu/~vakil/files/puzzle.gif
divertente vero?
http://math.stanford.edu/~vakil/files/puzzle.gif
divertente vero?
Il triangolo rosso e quello verde non sono simili (i rapporti tra i cateti sono 8/3 e 5/2 e 8/3>5/2)... così le due ipotenuse non sono tra loro parallele e la figura intera, che sembra un triangolo, in realtà è un quadrilatero concavo nel primo caso e convesso nel secondo (finalmente ho capito il perchè di questo apparente paradosso... non ci avevo mai pensato).
- Nonno Bassotto
- Site Admin
- Messaggi: 970
- Iscritto il: 14 mag 2006, 17:51
- Località: Paris
- Contatta:
Esiste anche un effetto meno appariscente, ma matematicamente più bello, anche perché generalizzabile a tutti i numeri di Fibonacci: si prende un quadrato di lato F(n) (n-esimo numero di Fibonacci), lo si scompone in modo opportuno ottenendo un retangolo di lati F(n+1)xF(n-1); il fatto è che le aree dei due quadrilateri differiscono di un'unità ...
Qui c'è l'esempio per n=8 (preso da Base5)
Ma al di là del motivo del perché salta fuori la differenza è interessante chiedersi dove sia andata a finire (o da dove sia saltata fuori) quell'unità in più.
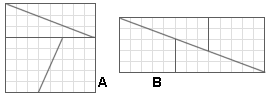
Qui c'è l'esempio per n=8 (preso da Base5)
Ma al di là del motivo del perché salta fuori la differenza è interessante chiedersi dove sia andata a finire (o da dove sia saltata fuori) quell'unità in più.

"Caso è lo pseudonimo usato da Dio quando non vuole firmare col proprio nome"
Attenzione! :shock:
L'inghippo sta nel fatto che le due figure non sono triangoli, ma quadrilateri, in particolare il "triangolo" superiore ha l' "ipotenusa" concava, l'altro "convessa" da cui la differenza di superficie.
Altro (e qui viene il bello) e' dimostrare secondo quali condizioni la differenza coincide con un quadratino perfetto...
coraggio!
L'inghippo sta nel fatto che le due figure non sono triangoli, ma quadrilateri, in particolare il "triangolo" superiore ha l' "ipotenusa" concava, l'altro "convessa" da cui la differenza di superficie.
Altro (e qui viene il bello) e' dimostrare secondo quali condizioni la differenza coincide con un quadratino perfetto...
coraggio!
Spelleg
Dimostrazione
L'area dei singoli componenti del quadrilatero concavo e' 32. L'area del triangolo in cui e' iscritto e' 32,5 (13x5/2)
Quindi la "fetta" concava ha area 0,5
Quando il quadrilatero diventa convesso, la fetta convessa e' speculare alla prima, e quindi 0,5x2= 1
Spero di essere stato chiaro, un disegno sarebbe assai piu' eloquente
Quindi la "fetta" concava ha area 0,5
Quando il quadrilatero diventa convesso, la fetta convessa e' speculare alla prima, e quindi 0,5x2= 1
Spero di essere stato chiaro, un disegno sarebbe assai piu' eloquente
@bolzo88 sì certo è proprio così,anche se l' angolo è impossibile da notare ad occhio nudo, con un pò di attenzione puoi però notare che l"ipotenusa" del "triangolo" in basso è più alta (guarda i quadratini) di quella della figura sopra, dunque siamo difronte a quadrilateri uno convesso e l' altro concavo.
@spelleg
@rdellab è tutto chiaro ma
@nonno bassotto
@spelleg
è proprio questo il bello delle figure.Altro (e qui viene il bello) e' dimostrare secondo quali condizioni la differenza coincide con un quadratino perfetto...
@rdellab è tutto chiaro ma
quando diventa concavo vorrai dire (quello sotto).Quando il quadrilatero diventa convesso
@nonno bassotto
mi piacerebbe sapere chi ha costruito il gioco per primo ma non credo sia Fibonacci.Credo che questa costruzione sia dovuta a Fibonacci.
Ultima modifica di herbrand il 16 giu 2006, 15:48, modificato 2 volte in totale.
La concavita' (o convessita') e' facile da dimostrare:
si osserva che tra i due triangoli non c'e' la proporzione tra i due cateti (3/8 il rosso, 2/5 il verde), condizione che ti garantisce di avere lo stesso angolo e quindi che le due ipotenuse dei triangoli di scomposizione costituiscano effettivamente l'ipotenusa del triangolo (virtuale) maggiore (cateti 5/13)
(peccato non riuscire ad inserire delle immaginette...)
si osserva che tra i due triangoli non c'e' la proporzione tra i due cateti (3/8 il rosso, 2/5 il verde), condizione che ti garantisce di avere lo stesso angolo e quindi che le due ipotenuse dei triangoli di scomposizione costituiscano effettivamente l'ipotenusa del triangolo (virtuale) maggiore (cateti 5/13)
(peccato non riuscire ad inserire delle immaginette...)
Spelleg