Teorema di Pitagora

[fede90]

Come tutti sanno, il celebre teorema di Pitagora afferma che in un triangolo rettangolo, dette $ $a,b,c$ $ le lunghezze rispettivamente dei due cateti e dell'ipotenusa, vale $ $a^2+b^2=c^2$ $. Le dimostrazioni sono moltissime (nel libro "The pythagorean proposition" il matematico Elisha Scott Loomis ne propose 367), quindi la mia idea era di raccogliere in questo topic il maggior numero possibile di dimostrazioni del suddetto teorema. Ognuno che ne avesse voglia, quindi, aggiunga una dimostrazione!

[SkZ]

data la relazione
$ $c^2=a^2+b^2-2ab\cos{\gamma} $
che lega i 3 lati di un triangolo a,b e c e l'angolo $ ~\gamma $ opposto ad c

Se c e' l'ipotenusa allora $ ~\gamma=\pi/2 $, quindi $ $a^2+b^2=c^2 $

[Stex19]

applicando il primo teorema di euclide a entrambi i cateti e sommando i risultati si ottiene pitagora.

[pak-man]

Poniamo in C l'angolo retto
Per il teorema dei seni abbiamo che $ a^2=c^2\displaystyle\frac{\sin^2\alpha}{\sin^2\gamma} $ e $ b^2=c^2\displaystyle\frac{\sin^2\beta}{\sin^2\gamma} $
Sommando membro a membro si ha $ a^2+b^2=c^2\displaystyle\frac{\sin^2\alpha+\sin^2\beta}{\sin^2\gamma} $
$ \gamma $ è retto, quindi $ \beta=\pi/2-\alpha $ e $ \sin^2\alpha+\sin^2\beta=\sin^2\alpha+\cos^2\alpha=1 $.
Semplificando il tutto si ottiene la tesi.

[pak-man]

Dimostrazione algebrica (non sono molto sicuro, correggetemi se sbaglio).
Poniamo i cateti del triangolo allineati con gli assi del piano di Gauss: allora $ a+bi=ce^{i\phi} $.
Consideriamo il coniugato: $ a-bi=ce^{-i\phi} $.
Moltiplichiamo e otteniamo la tesi.

[fede90]

$ \sin^2\alpha+\cos^2\alpha=1 $

Ecco, mi sorge un dubbio: la relazione sopracitata non deriva dal teorema di Pitagora? Quindi non è assurdo dimostrare il teorema di Pitagora usando una relazione che si dimostra a sua volta con il teorema di Pitagora?

[bestiedda]

data la relazione
$ $c^2=a^2+b^2-2ab\cos{\gamma} $
che lega i 3 lati di un triangolo a,b e c e l'angolo $ ~\gamma $ opposto ad c

Se c e' l'ipotenusa allora $ ~\gamma=\pi/2 $, quindi $ $a^2+b^2=c^2 $

anche nella dimostrazione di questo c'è il teorema di pitagora

poi magari è dimostrabile anche senza, non so

[julio14]

Ma credo che tutte le dimostrazioni finora citate si servano del teorema di pitagora, a parte euclide, di cui praticamente è un corollario. Queste due costruzioni dimostrano abbastanza facilmente la prima euclide, e quindi pitagora, e la seconda direttamente pitagora.

[Haile]

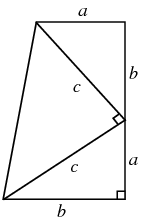
L'area del trapezio in figura è pari a

$ $\frac{1}{2}(a+b)(a+b) = \frac{1}{2}(a^2 + 2ab + b^2)$ $

Ma se calcoliamo l'area sommando le aree dei tre triangoli otteniamo invece

$ $\frac{1}{2}ab + \frac{1}{2}ab + \frac{1}{2}c^2$ $

Uguagliando le due espressioni, riarrangiando e fattorizzando:

$ $\frac{1}{2}(a^2 + b^2 + 2ab) = ab + \frac{1}{2}c^2$ $

$ $a^2 + b^2 + 2ab = 2ab + c^2$ $

quindi

$ $\boxed{a^2 + b^2 = c^2}$ $

Garfield (1876)

[fede90]

Ma credo che tutte le dimostrazioni finora citate si servano del teorema di pitagora, a parte euclide, di cui praticamente è un corollario.

Eh infatti... Comunque ve ne propongo una che ho trovato un giorno praticamente per caso. Il principio è semplice: trovo il raggio della circonferenza inscritta in due modi diversi e poi eguaglio.

Sia $ $r$ $ il raggio della circonferenza inscritta. Dalla congruenza tra $ $AOH$ $e $ $AOG$ $ si ha $ $AH=AG$ $ e analogamente $ $BF=BG$ $, da cui $ $AH+BF=c$ $. Ma poichè $ $CH=CF=r$ $, abbiamo $ $BF=a-r$ $ e $ $AH=b-r$ $. Eguagliando si ha $ $r=(a+b-c)/2$ $.
Sappiamo poi che il raggio del cerchio inscritto in un poligono è, in generale, $ $r=S/p$ $. Sostituendo $ $S=ab/2$ $ e $ $p=(a+b+c)/2$ $ otteniamo $ $r=ab/(a+b+c)$ $. Eguagliando le due espressioni trovate per $ $r$ $ otteniamo, guarda un po', il teorema di Pitagora.

[edriv]

La mia preferita è questa:
è chiaro che $ [ABH] + [ACH] = [ABC] $(si parla di aree, A è l'ipotenusa).
essendo ABH,ACH,ABC triangoli simili di ipotenusa AB,AC,BC, è altrettanto chiaro che moltiplicando la relazione di sopra per un'opportuna costante, otteniamo:
$ ~ AB^2 + AC^2 = BC^2 $.

[julio14]

bellissima!!!

[bigelf90]

Scusate 1 cosa: ma dimostrando il teorema dei seni dimostrerei necessariamente anche pitagora? Se si, 1 dimostrazione potrebbe essere questa

[julio14]

mmm non ho molto capito cosa vuoi dire... ti riferisci alla soluzione di pak-man? Quella usa $ $\sin^2\alpha+\cos^2\alpha=1 $, che è pitagora.

[mitchan88]

Quella contosa ma più generale (con $ ( , ) $ si intende il prodotto scalare standard)
Siano $ a,b,c $ i vettori dei punti A,B,C. Il fatto che $ \angle ABC $ sia retto si scrive $ 0=(a-b,c-b)=(a,c)-(a,b)-(b,c)+|b|^2 $
Ora $ \displaystyle |a-b|^2+|b-c|^2=(a-b,a-b)+(b-c,b-c)= $
$ =|a|^2+|c|^2+2(|b|^2-(a,b)-(b,c))=|a|^2+|c|^2-2(a,c)=|a-c|^2 $